Rappelons que les résolutions sont emboîtées les unes dans les autres. On peut donc définir le supplémentaire orthogonal Wj de Vj dans Vj-1 :
Alors il existe une fonction y telle que la famille yj,n(t) = 2-j/2 y(2-jt-n), n décrivant Z, soit une base orthonormée de Wj. La familles des yj,n, j et n décrivant Z, est une base orthonormée de L2 et
y est une ondelette orthogonale associée à l'approximation multirésolution. Un signal f de L2 se décompose en
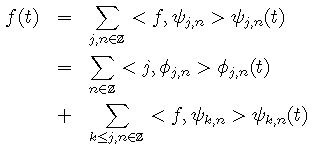
où f est une fonction d'échelle orthogonale de la multirésolution.
Un théorème de Mallat et Meyer permet de construire une ondelette à partir de la fonction d'échelle.
Voici une fonction d'échelle spline cubique et l'ondelette spline cubique de Battle-Lemarié correspondante, ainsi que leurs transformées de Fourier. L'ondelette est un spline cubique car combinaison linéaire localement finie de splines cubiques.
L'ondelette n'est pas à support compact.
Les bases d'ondelettes sont des bases de L2(R). Il existe plusieurs méthodes pour les transformer en bases d'ondelettes sur l'intervalle. Après discrétisation, elles se prêtent au traitement des signaux finis.
Il existe plusieurs méthodes pour construire des bases d'ondelettes pour des espaces de fonctions à plusieurs variables. La plus simple consiste à construire des ondelettes séparables.