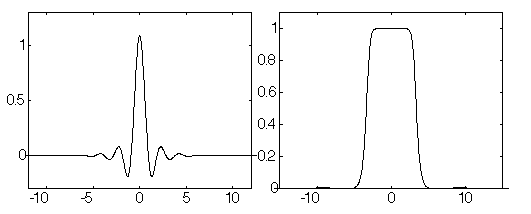
On peut transformer la base de Riesz en une base orthogonale obtenue par des translations entières d'une fonction élémentaire, qu'on appelle fonction d'échelle (orthogonale). C'est un cas de système de multirésolutions biorthogonales où les deux multirésolutions et les deux bases de Riesz sont confondues.

Il est facile de voir que les autres résolutions sont engendrées par des dilatations adéquates de cette base d'atomes translatés. Comme les résolutions sont emboîtées les unes dans les autres, il existe nécessairement une suite de réels h[n] telle que
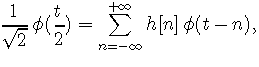
soit, dans le domaine de Fourier
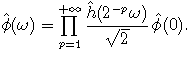
en supposant la transformée de Fourier continue.
On montre h est un filtre miroir conjugué. Il détermine entièrement la fonction d'échelle et la plupart de ses propriétés. En particulier, la fonction d'échelle est à support compact si et seulement si h a un nombre fini de coefficients non nuls. On dit alors que h est un filtre à réponse impulsionnelle finie. Pour plus de détails, se reporter à la page sur les propriétés des ondelettes orthogonales et leur lien avec le filtre h.
A titre d'exemple, on donne les coefficients du filtre h correspondant à la fonction d'échelle spline cubique précédente.
L'étude des filtres h conduisant à des approximations multirésolutions a donné lieu à de nombreux et importants théorèmes. Le premier d'entre eux donne des conditions nécessaires et suffisantes pour que h engendre une fonction d'échelle:
La condition (7.35) signifie que h est un filtre miroir conjugué. La condition (7.36) est une simple normalisation. La condition (7.37) permet de vérifier que la fonction définie par (7.38) est bien d'énergie finie.
L'équation d'échelle montre que les coefficients d'échelle a1 [n] = < a , j(t/2-n) > de a dans V1 s'obtiennent à partir des coefficients d'échelle a0 [n] = < a , j(t-n) > dans V0 par convolution avec le filtre miroir conjugué h et sous-échantillonnage:
Retour aux approximations multirésolution