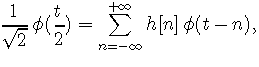
Lorsque la base de Riesz est une base orthogonale, l'approximation multirésolution est orthogonale, et l'atome de base est appelée fonction d'échelle. Il est toujours possible d'orthogonaliser une approximation multirésolution.
Néanmoins, l'orthogonalité impose des contraintes qui peuvent ne pas être désirables. L'une des plus importantes est qu'une fonction d'échelle f orthogonale à support compact ne peut être symétrique et continue. La propriété de symétrie est utile pour l'analyse des signaux de longueur finie.
Certaines de ces restriction (notamment sur la symétrie) peuvent être levées en utilisant des approximations multirésolutions biorthogonales.
La dénomination "approximation" signifie qu'à une analyse (ou approximation) multirésolution orthogonale ou biorthogonale on peut associer une suite de projecteurs respectivement orthogonaux ou obliques, qui approximent efficacement les signaux réguliers. L'ordre d'approximation est liée au degré des polynômes reconstituables par les résolutions.
Les analyse multirésolutions sont déterminées par le ou les atomes f qui engendrent respectivement l'approximation multirésolution orthogonale ou la paire de multirésolutions biorthogonales.
Par définition de la multirésolution, f(t/2) est une combinaison linéaire des f (t-n). On parle d'équation d'échelle:
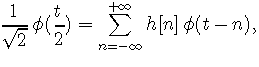
Dans le domaine fréquentiel, cela donne
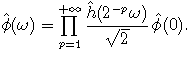
Les coefficients h[n] de l'équation d'échelle déterminent f entièrement, et leur calcul revient à la conception d'un banc de filtres, plus des conditions de stabilité pour pouvoir engendrer L2.
Plus l'échelle j est fine, plus l'approximation est précise (voir Lena). En passant d'une échelle j à une échelle j-1, on rajoute des détails au signal. De même que les approximations peuvent décomposer dans une base de résolution, ces détails supplémentaires peuvent se décomposer dans des bases de détails.
Ces espaces de détails sont, comme les résolutions, engendrés par les translatées d'une unique fonction. Cette fonction s'appelle une ondelette. L'ordre d'approximation de la multirésolution correspond au nombre de moments nuls de l'ondelette. Il représente également la capacité de l'ondelette à détecter les singularités isolées d'un signal.