
g et h sont des filtres miroirs conjugués.
Les filtres miroirs conjugués sont un cas particulier des bancs de filtres à reconstruction parfaite. La nature dyadique de l'approximation multirésolution est étroitement liée à la possibilité d'opérer des sous-échantillonnages élémentaires du signal par suppression d'un terme sur deux, et des suréchantillonnages élémentaires par insertion d'un zéro tous les deux coefficients.
Le calcul des coefficients a1 [n] et d1 [n] d'un signal dans Vj et Wj à partir de ses coefficients a0[n] dans Vj-1 se fait par application des filtres miroirs conjugués puis par un sous-échantillonnage:
en posant h1[n] = h[-n] et g1[n] = g[-n].

Les coefficients de h sont donnés par l'équation d'échelle

c'est-à-dire, dans le domaine fréquentiel:
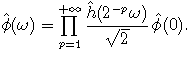
et les coefficients de g sont donnés par l'équation d'échelle sur l'ondelette:
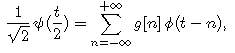
soit, dans le domaine fréquentiel:
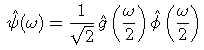
En pratique, cette récurrence est initialisée en assimilant les échantillons du signal aux coefficients de résolution la plus fine.
Inversement, la reconstruction de a0[n] à partir de a1 [n] et de d1 [n] se fait en insérant un zéro entre chaque échantillon puis en faisant la somme des convolutions avec h et g:
où l'opérateur z représente l'insertion de zéro.

L'évaluation des diverses ondelettes et fonctions d'échelles de fait comme dans le cas orthogonal.
La construction d'ondelettes orthogonales revient donc à la synthèse de filtres miroirs conjugués possédant une propriété de stabilité.
On s'intéressera au cas particulier des filtres à réponse impulsionnelle finie, i.e., aux ondelettes à support compact.