These few examples are based on the same synthetic signals as for the windowed Fourier transform.
They illustrate the wavelet transform's ability to localize instaneous frequencies.
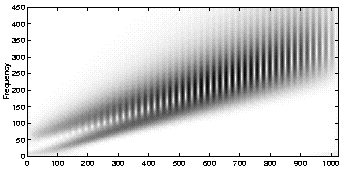
Here is the sum of two parallel linear chirps with its scalogram. When the frequency increases, the frequency resolution of the transform decreases.

Here is the normalized scalogram and the complex phase of the wavelet transform of a synthetic signal which is the sum of a linear chirp with an increasing frequency, a quadratic chirp with a decreasing frequency, and two modulated gaussians. Their computations have been performed with a Gabor wavelet.
The makup of this signal explicitly introduces instantaneous frequencies.
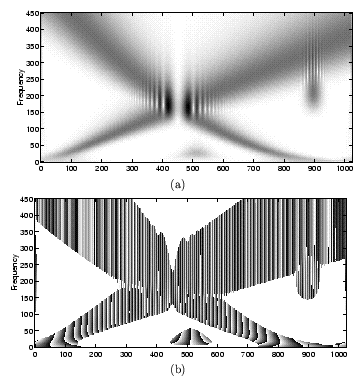
Here is the sum of two hyperbolic chirps and its scalogram.
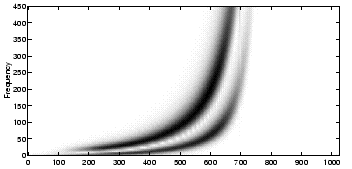
In the first example, the instantaneous frequencies are more blurred in the scalogram than in the spectrogram. On the other hand, the variable time resolution of the wavelet transform makes it possible to track the hyperbolic frequency across time. The decreasing frequency resolution is masked by the vertical asymptotic tendency.