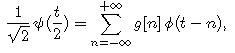
Dilated wavelets are related by a scaling equation.
Rescaling can be interpreted as discrete filtering.
Vanishing moments, support, regularity and symmetry of the wavelet and scaling function are determined by the scaling filter.
y(t/2) and f(t) are related by a scaling equation, similar to the equation which relates j(t/2) and j(t). It is a consequence of (7.60):
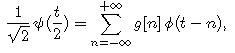
In the Fourier domain, this equation becomes
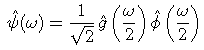
The h and g filters are a conjugate mirror filter bank.
A wavelet has m vanishing moments if and only if its scaling function can generate polynomials of degree smaller than or equal to m. While this property is used to describe the approximating power of scaling functions, in the wavelet case it has a "dual" usage, e.g. the possibility to caracterize the order of isolated singularities.
The number of vanishing moments is entirely determined by the coefficients h[n] of the filter h which is featured in the scaling equation.
If the Fourier transform of the wavelet is p continuously differentiable, then the three following conditions are equivalent:
Compactly supported wavelets and scaling functions exist.
The scaling function is compactly supported if and only if the filter h has a finite support, and their supports are the same. If the support of the scaling function is [N1,N2], then the wavelet support is [(N1-N2+1)/2,(N2-N1+1)2].
Atoms are thus compactly supported if and only if the filter h is.
Daubechies has proved that, to generate an orthogonal wavelet with p vanishing moment, a filter h with minimum length 2p had to be used. Daubechies filters, which generate Daubechies wavelets, have a length of 2p. The Daubechies filter coefficients are available as ASCII text files which can be used in a spreadsheet, for instance.
Wavelet regularity is much less important than their vanishing moments. Il is studied in a theorem by Tchamitchian
The following two properties are important:
Meyer wavelets are indefinitely differentiable orthogonal wavelets, with an infinite support. They are generally implemented in the Fourier domain.
Symmetric scaling functions and wavelets are important because they are used to build bases of regular wavelets over an interval, rather than the real axis. Daubechies has proved that, for a wavelet to be symmetric or antisymmetric, its filter must have a linear complex phase, and the only symmetric compactly supported conjugate mirror filter is the Haar filter, which corresponds to a discontinuous wavelet with one vanishing moment. Besides the Haar wavelet, there is no symmetric compactly supported orthogonal wavelet.