
g and h are conjugate mirror filters.
Conjugate mirror filters are a particular instance of perfect reconstruction filter banks. The dyadic nature of multiresolution approximations are closely related to the possibility of implementing elementary signal subsampling by erasing one sample every two, and elementary oversampling by zero insertion between two consecutive samples.
The coefficients 1 [n] and d1 [n] of a signal in Vj and Wj are computed from its coefficients a0[n] in Vj-1 by applying conjugate mirror filters and subsampling the output:
with h1[n] = h[-n] and g1[n] = g[-n].

In practice this recursion is initialized by considering that the discrete signal samples are some fine resolution coefficients.
The coefficients of h are defined by the scaling equation

or, in the Fourier domain:
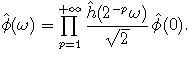
and the coefficients of g are defined by the wavelet scaling equation
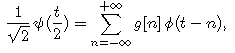
or, in the Fourier domain:
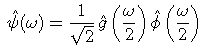
Conversely, a0[n] is reconstructed from a1 [n] and d1 [n] by inserting zeroes between two consecutive samples and summing their convolutions with h and g:
where the z operator represents the insertion of zeroes.

Wavelets and scaling functions are evaluated as in the orthogonal case.
Hence the construction of orthogonal wavelets is equivalent to the synthesis of conjugate mirror filters having a stability property.
We will concentrate on Finite Impulse Response filters, e.g., to compactly supported wavelets.