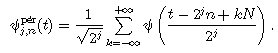
On n'a considéré dans les autres pages que des ondelettes sur l'axe réel, c'est-à-dire des ondelettes adaptées à l'analyse de signaux définis sur tout l'axe. Dans la plupart des cas, les signaux sont à support compact; notamment les images, qui sont explicitement définies sur une rectangle de pixels.
On supposera ici les ondelettes à support compact.
Un signal à support sur [0,N] peut se représenter comme le produit d'un signal par la fonction caractéristique de [0,N]. Les discontinuités de cette fonction nécessite un traitement particulier. On connaît trois méthodes dont la troisième est la plus efficace.
Les ondelettes sont périodisées par la formule:
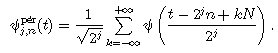
avec j<=log2N. Cette méthode revient à périodiser le signal.
Les ondelette situées bien à l'intérieur de l'intervalle ne sont pas modifiées. Celles proches du bords se retrouvent découpées en deux morceaux collés aux bords gauches et droits. Chaque morceau, pris séparément, n'a pas de moment nul. Cela donne de grands coefficients d'ondelettes lorsque le signal périodisé n'est pas continu.
Pour éviter ce problème, on replie le signal par symétrie autour du bord droit, et on périodise le signal sur l'intervalle double.
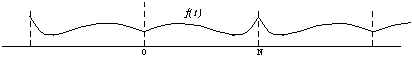
Le signal obtenu est continu.
En traduisant la transformation de f en une transformation sur la base d'ondelettes, on voit que la famille de vecteurs est une base de L2[0,N] si l'ondelette est symétrique ou antisymétrique. Cela écarte les ondelettes orthogonales.
En fait, on n'a fait que repousser le problème à la dérivée suivante. La méthode suivante s'attaque au problème de base, qui est la nullité des moments des ondelettes sur l'intervalle.
On gère explicitement les effets de bord. On considère une base orthogonale de Daubechies à p moments nuls.
D'après les conditions de Strang et Fix, il existe un polynôme qk de degré k tel que:
pour k<p.
On multiplie cette identité par la fonction caractéristique de [0,N]. En supposant que le support de j est [-p+1,p], les fonction d'échelles d'indice p<=k<N-p sont inchangées par la restriction. Pour retrouver la condition de Strang et Fix sur l'intervalle, on cherche p fonctions d'échelle "gauches" et p fonctions d'échelles "droites" telles que
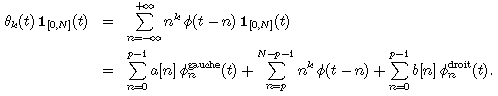
Si cette égalité est vérifiée, elle est encore vraie après changement d'échelle, car les nk, à une puissance de 2 près, sont les coefficients d'échelle de qk à toutes les résolutions. Il reste à trouver les filtres h et H réalisant l'équation d'échelle:
où 
désigne
l'ensemble des fonctions d'échelle obtenues par dilatation
à la résolution j, ainsi que la condition
d'orthogonalité.
Les coefficients des filtres sont disponibles sous Wavelab par la fonction MakeCDJVFilter.