Comme en dimension 1, l'analyse des maxima dyadiques permet de détecter les singularités.
A condition de tenir compte de la géométrie en dimension 2, celles-ci peuvent s'interpréter comme des contours.
Un algorithme analogue à celui de la dimension 1 permet de reconstituer une bonne approximation de l'image à partir de ses contours.
Dans une image, on perçoit le plus souvent comme des bords des lignes le long desquels se produit une brusque variation d'intensité de la lumière. Pour simplifier, on supposer l'image monochrome. Bien que la notion réelle de bord soit plus complexe et dépende en particulier de connaissances a priori sur l'objet rechercher, elle présente l'avantage de conduire à définition mathématique rigoureuse d'un "point de bord".
Pour cela, on prend une ondelette en dimension deux définie par dérivation partielle d'un noyau:
La transformée en ondelettes dyadique utilisée est
avec, pour k=1,2,
Les deux coordonnées de la transformée dyadique sont le gradient de la convolution du signal avec le noyau dilaté:
Les points de contours multiéchelles sont les points de où le module de la transformée en ondelettes dyadique est maximal dans la direction pointée par le vecteur précédent. Cela correspond à une vitesse de variation localement maximale le long de la normale aux courbes d'isohélie.
Un exemple de synthèse analyse les contours d'un cercle.
Un autre exemple analyse une photo classique de la théorie des ondelettes.
Il est rare, dans une image, qu'une ligne de contour ne présente pas des trous. Le cerveau comble ces lacunes grâce une analyse plus complexe de l'image. Notons, à ce propos, que l'utilisation de la couleur peut améliore les choses. A titre d'illustration, voici une illusion d'optique où l'on serait bien en peine de décider où détecter des contours:

Comme en dimension 1, on peut utiliser l'opérateur de frame inverse pour reconstruire une image de norme minimal de valeurs prescrites sur les lieux des maxima. On obtient des erreurs relatives quadratiques moyennes de l0-2.
Sur un exemple, on voit que l'erreur de reconstruction est négligeable.
Les calculs sont effectués avec des ondelettes séparables de transformées de Fourier
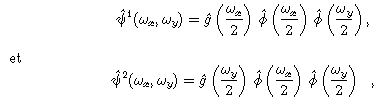
ou le filtre g est un filtre de différence finie; les deux ondelettes sont alors des approximations des dérivées partielles de
où f est une fonction d'échelle définie par un filtre h à réponse impulsionnelle finie. La transformée en ondelettes dyadique est calculée par une extension à la dimension 2 de l'algorithme à trous.