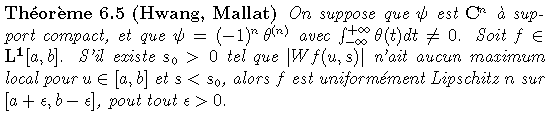
Les maxima du module de la transformée en ondelettes sont liées aux singularités du signal.
Plus précisément, le théorème suivant montre qu'il ne peut y avoir de singularité sans maximum local de la transformée en ondelettes dans les échelles fines.
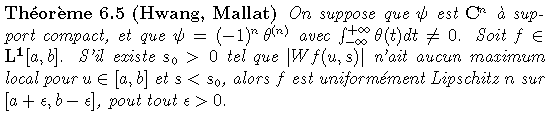
Ce théorème indique la présence d'un maximum dans les échelles fines en cas de singularité. En général, on détecte une suite de modules maximaux convergeant vers la singularité. Voici les modules maximaux de l'exemple précédent:
Attention: il s'agit ici des maxima du module de la transformée; les fréquences instantanées se détectent, elles, en suivant les maxima du scalogramme normalisé:
qui
comporte deux différences: la normalisation, et le fait que la
variable utilisée soit homogène à une
fréquence, et non à une échelle.
Dans le cas où l'ondelette est la dérivée nème d'une gaussienne, les courbes de maxima sont connexes et continuent jusqu'aux échelles les plus fines.
Le taux de décroissance des maxima les long des courbes indique l'ordre des singularités isolées (c'est une conséquence des théorèmes 6.5 et 6.4 étendu à l'intervalle):
Graphiquement, on trace les modules maximaux en fonction de l'échelle dans un diagramme log-log, et la pente donne l'ordre de singularité estimé. Voici cette courbe pour deux singularités: en trait plein, pour la singularité en t=14, et en pointillés, pour la singularité en t=108. Les échelles fines sont à gauche.
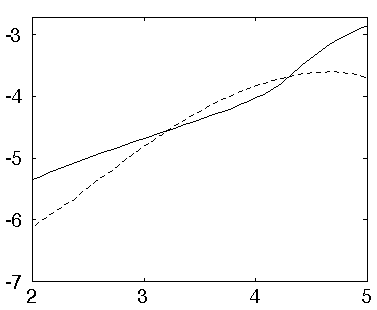
Pour t=14, la pente vaut 1/2, et donc la fonction y est Lipschitz 0, c'est-à-dire une discontinuité. En t=108, on a à peu près une pente de 1, et donc la fonction y est Lipschitz 1/2.