Periodic input estimation for linear periodic systems: Automotive engine applications
Auteurs: Jonathan Chauvin, Gilles Corde, Nicolas Petit et Pierre Rouchon
Automatica. Vol. 43, No. 6, pp 971--980. 2007, DOI: 10.1016/j.automatica.2006.12.012
In this paper, we consider periodic linear systems driven by T0 -periodic signals that we desire to reconstruct. The systems under consideration are of the form
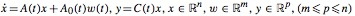
where A(t ), A0 (t ), and C(t ) are T0 -periodic matrices. The period T0 is known. The T0 -periodic input signal w(t ) is unknown but is assumed to admit a finite dimensional Fourier decomposition.
Our contribution is a technique to estimate w from the measurements y. In both full state measurement and partial state measurement cases, we propose an efficient observer for the coefficients of the Fourier decomposition of w(t ). The proposed techniques are particularly attractive for automotive engine applications where sampling time is short. In this situation, standard estimation techniques based on Kalman filters are often discarded (because of their relative high computational burden). Relevance of our approach is supported by two practical cases of application.
Detailed convergence analysis is also provided. Under standard observability conditions, we prove asymptotic convergence when the tuning PeriodicInputparameters are chosen sufficiently small.
Download PDF
Automatica. Vol. 43, No. 6, pp 971--980. 2007, DOI: 10.1016/j.automatica.2006.12.012
In this paper, we consider periodic linear systems driven by T0 -periodic signals that we desire to reconstruct. The systems under consideration are of the form
where A(t ), A0 (t ), and C(t ) are T0 -periodic matrices. The period T0 is known. The T0 -periodic input signal w(t ) is unknown but is assumed to admit a finite dimensional Fourier decomposition.
Our contribution is a technique to estimate w from the measurements y. In both full state measurement and partial state measurement cases, we propose an efficient observer for the coefficients of the Fourier decomposition of w(t ). The proposed techniques are particularly attractive for automotive engine applications where sampling time is short. In this situation, standard estimation techniques based on Kalman filters are often discarded (because of their relative high computational burden). Relevance of our approach is supported by two practical cases of application.
Detailed convergence analysis is also provided. Under standard observability conditions, we prove asymptotic convergence when the tuning PeriodicInputparameters are chosen sufficiently small.
Download PDF